7. Ley de gravitación universal

La ley de la gravitación universal, o simplemente, ley de la gravedad, establece la fuerza con la que se atraen dos cuerpos por el simple hecho de tener masa. Esta ley fue desarrollada por Sir Isaac Newton en el tercer libro de su obra Principios matemáticos de fillosofía natural, titulado Sobre el sistema del mundo.

Fuerza de la gravedad

La expresión de la ley de gravitación universal se plasma en la expresión de la fuerza gravitatoria o fuerza de la gravedad, ya estudiada en niveles anteriores (puedes pulsar sobre la pestaña Ver también en la parte superior de la página para ampliar información a este respecto). En esta sección vamos a recordarla y a profundizar en ella.

Dos cuerpos se atraen con una fuerza directamente proporcional al cuadrado de sus masas e inversamente proporcional al cuadrado de la distancia que las separa, y está dirigida según la recta que une los cuerpos. Dicha fuerza se conoce como fuerza de la gravedad o fuerza gravitacional y se expresa de la forma:

F→g=−G⋅M⋅mr2⋅u→r

donde:

• F→g :Es el vector fuerza gravitatoria. Su unidad de medida en el Sistema Internacional es el newton (N)
• G es la constante de gravitación universal, que no depende de los cuerpos que interaccionan y cuyo valor es G = 6,67·10-11 N·m2/kg2, 
• M y m son las masas de los cuepos que interaccionan. Su unidad de medida en el Sistema Internacional (S.I.) es el kilogramo (kg)
• r es la distancia que los separa. Es el módulo del vector r→ , que une la masa que genera la fuerza con la masa sobre la que actúa.
• u→r es un vector unitario que posee la misma dirección de actuación de la fuerza aunque de sentido contrario.

Por tanto, la interacción gravitatoria entre dos cuerpos siempre se manifiesta como una pareja de fuerzas iguales en dirección y módulo pero sentido contrario. El caracter atractivo de la fuerza se indica mediante el signo - de la expresión anterior. La siguiente imagen ilustra este concepto. 

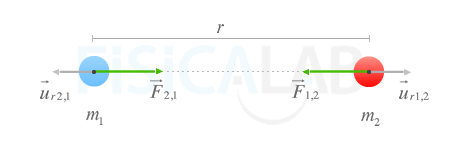
Fuerza Gravitacional

La segunda masa (m2) es la responsable de aparezca una fuerza de atracción sobre el primer cuerpo (m1) denominada F→2,1. Este a su vez también es el responsable de que aparezca una fuerza de atracción denominada F→1,2 sobre el cuerpo m1.  

Ambas fuerzas son de igual dirección aunque de sentido contrario. Vectorialmente podemos expresar esto diciendo que:

u→r1,2=−u→r2,1 ⇒ F→1,2 = −F→2,1

Efectos sobre un conjunto de masas

Hemos estudiado cómo la gravedad actúa sobre una pareja de cuerpos como una pareja de fuerzas, pero ¿qué ocurre cuando, en lugar de dos masas, tenemos tres o más?

La fuerza gravitatoria resultante que actúa sobre una masa cualquiera de un conjunto de más de dos masas se calcula, según el principio de superposición, calculando la resultante de las fuerzas gravitatorias que las demás ejercen sobre ella. 

Así, si por ejemplo tenemos n masas, la fuerza gravitatoria que actuará sobre la primera de las masas se calculará según:

F→1=F→2,1+F→3,1+…+F→n,1

La siguiente imagen ilustra el principio anterior.

Fuerza Gravitatoria Resultante

Las tres partículas de la figura interaccionan entre sí a través de la fuerza gravitatoria. Cada una de ellas experimenta un par de fuerzas, debido a las otras dos partículas, y a su vez genera una fuerza sobre cada una de ellas.